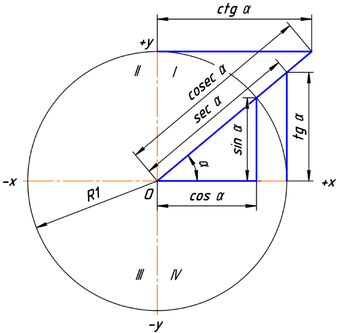
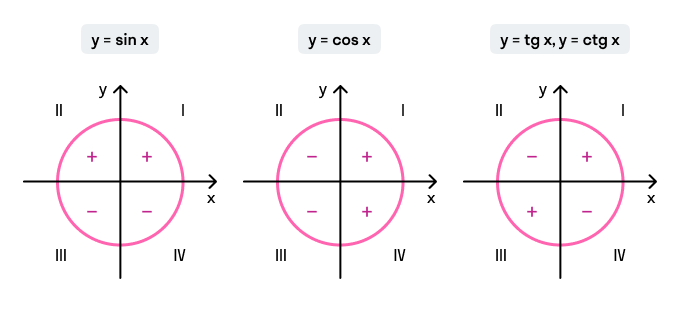
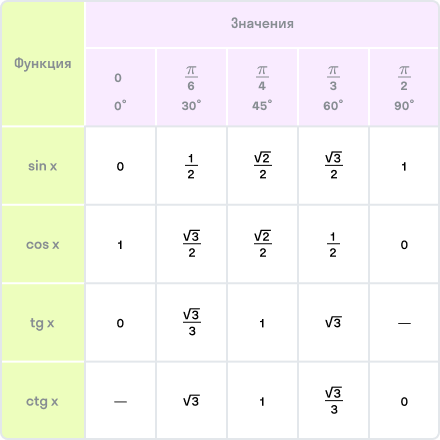
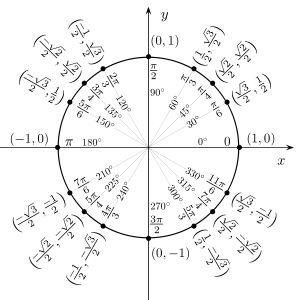
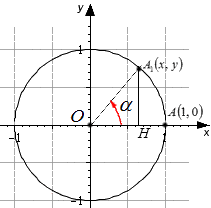
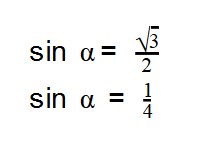Как связать синус и тангенс
Тригонометрия с нуля в 9 классе
Возможно, но и математика не покажется такой трудной, если узнать про экзамен побольше. В математике, как и в любом предмете, есть опорные темы. Для начала разбираемся с ней.

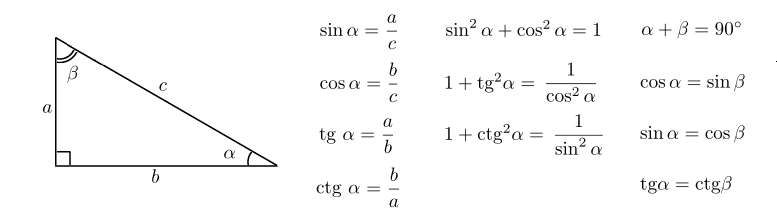




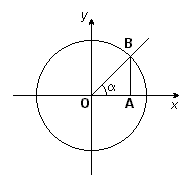


Справочник по MATLAB - Графические команды и функции (В.Г.Потемкин)
Приемы обучения учащихся выполнению тождественных преобразований тригонометрических выражений;. Тригонометрические преобразования — одна из самых сложных тем школьной программы. Одна из причин — множество формул в данном разделе.
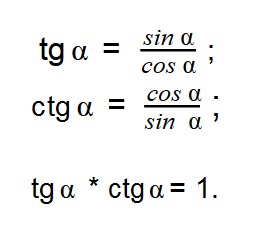




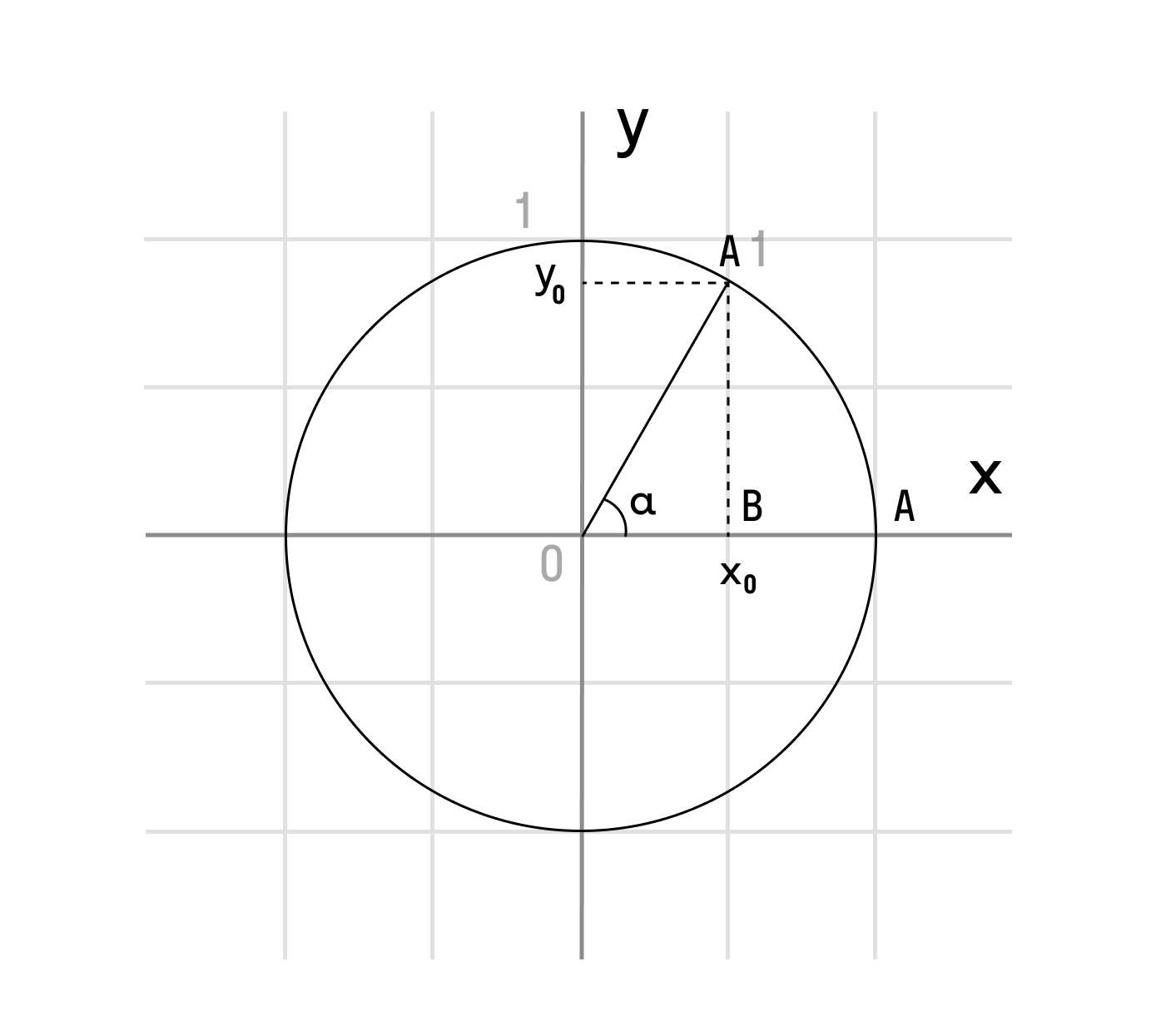


Тригонометрия начинается в 9-м классе и это одна из самых нелюбимых тем у школьников. Не потому, что она сложная, а потому, что это что-то новое и очень необычное. Но в ОГЭ она если и встречается, то в первой части, а значит, ничего сложного там не должно быть. Возникает интересный вопрос: как может пригодиться тригонометрия в реальной жизни? Оказывается, ее применение очень обширно: в астрономии и навигации при определении углов и направлений, в географии, в волновой физике радио, радары, свет, рентген и т.