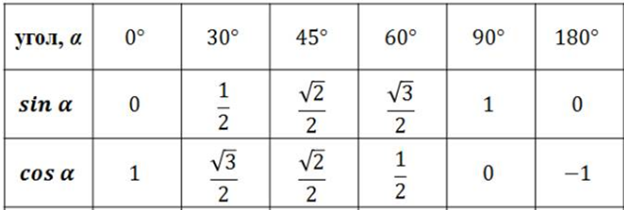
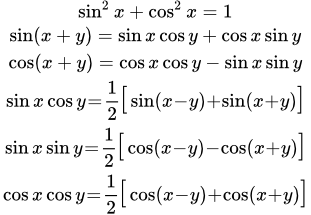Таблица Синусов И Косинусов Картинки
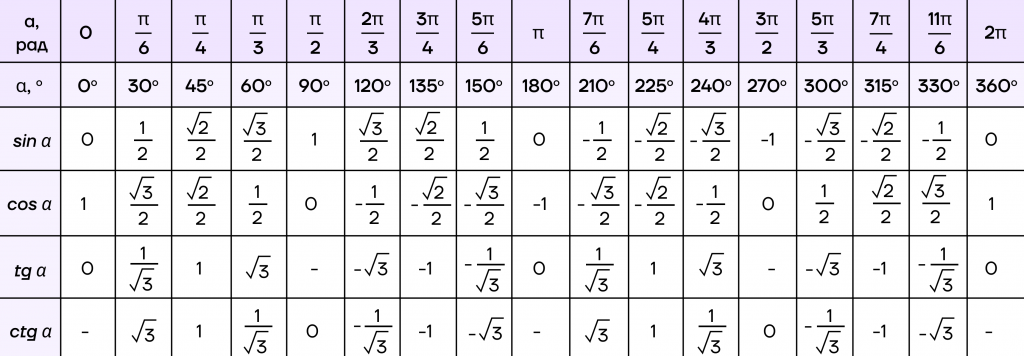
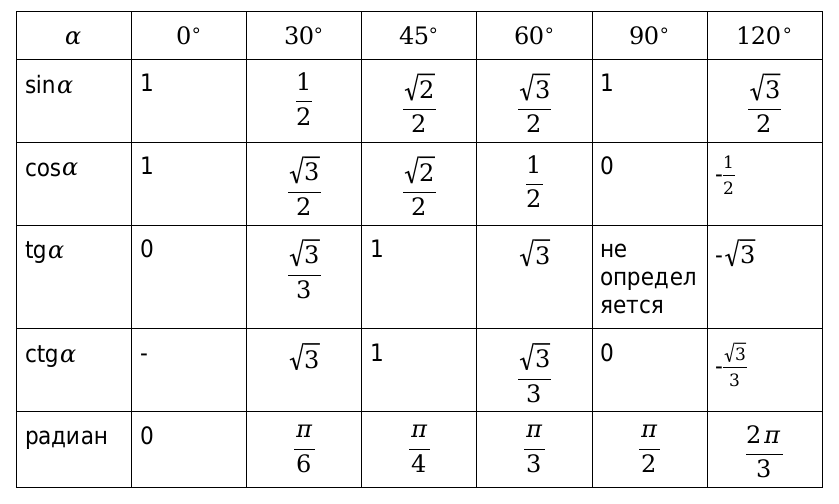
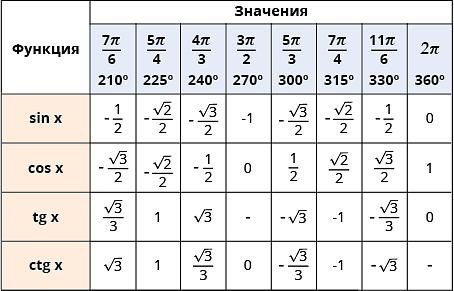
Таблица тригонометрии
Картинки » Синус косинус тангенс котангенс на рисунке. Синус косинус тангенс котангенс на рисунке - 73 фото 0 1 2 3 4 5. В этой подборке вы найдете 73 красивых и очаровательных картинок с на тему Синус косинус тангенс котангенс на рисунке.
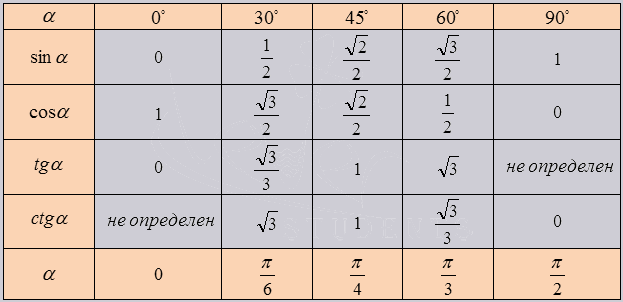






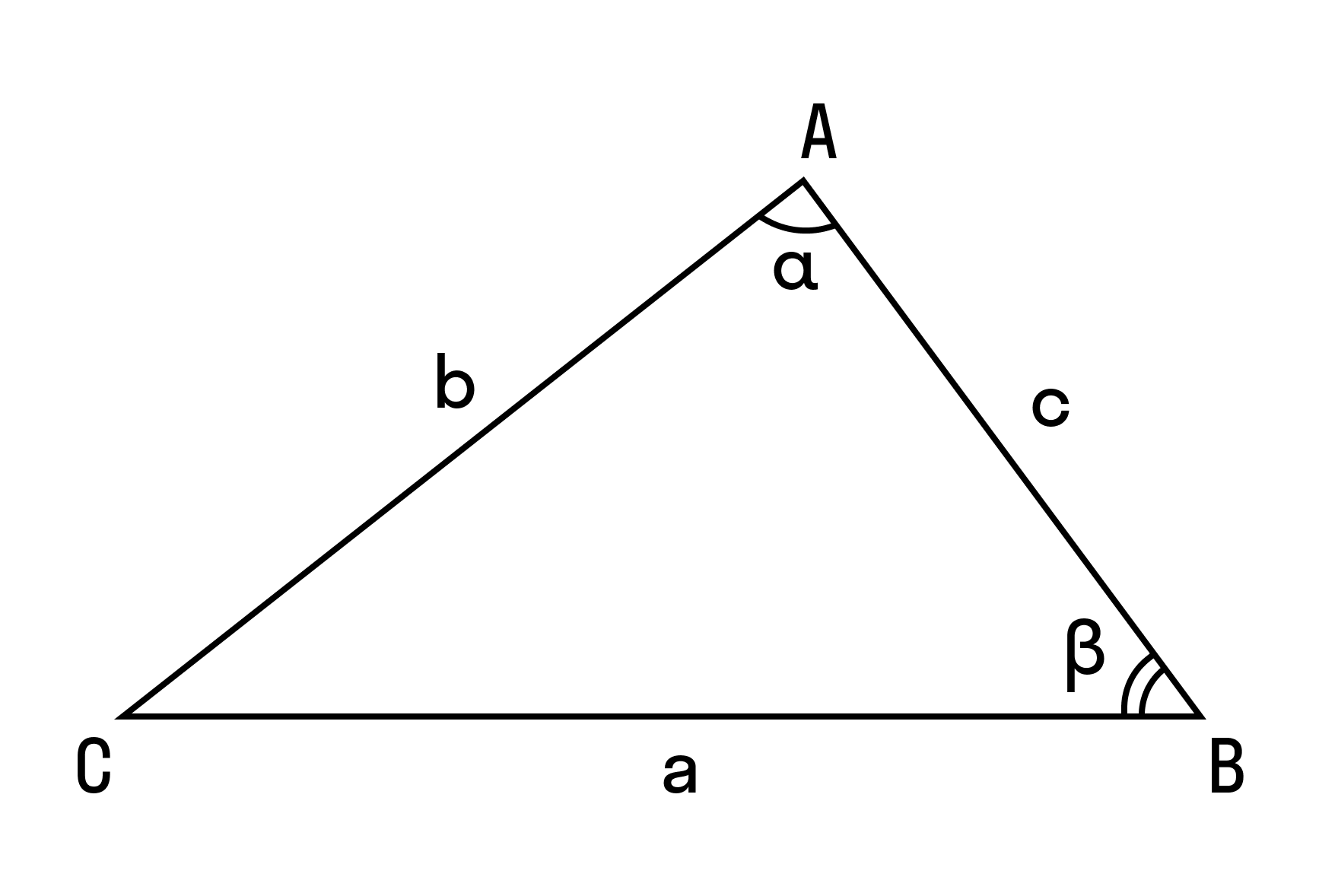
К этой теме имеются дополнительные материалы в Особом разделе Для тех, кто сильно "не очень Продолжаем осваивать таблицу синусов и косинусов. А именно - привыкаем работать с необходимыми табличными значениями без механической зубрёжки. И, разумеется, без бумажек-шпаргалок. Это несложно.

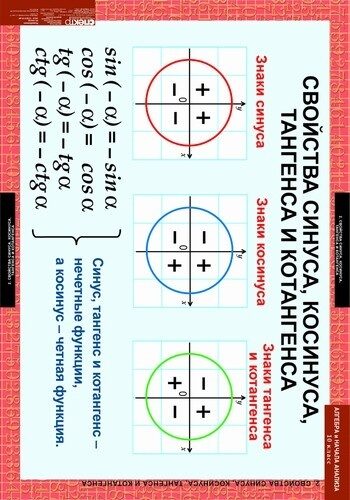
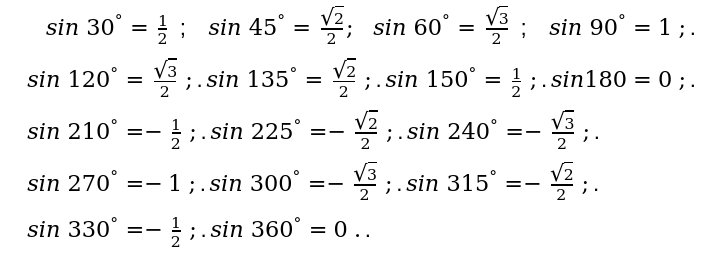


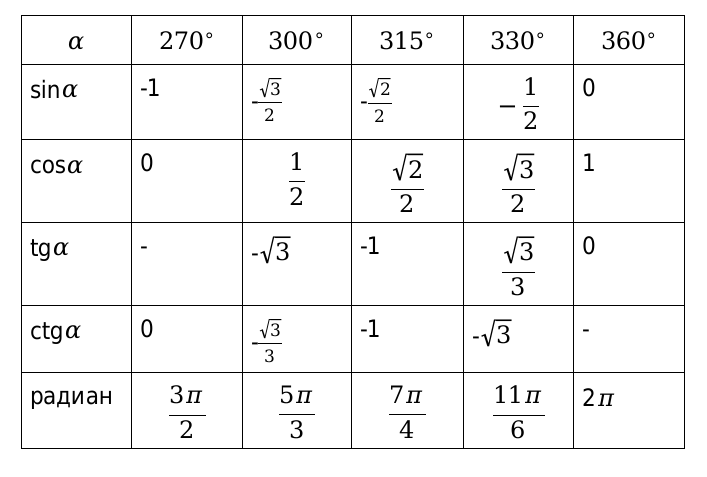



English EN. Калькулятор Интегралов. Решение Определенных и Неопределенных Интегралов первообразных. Калькулятор интегрирует функции, используя методы: замены, рациональных функций и дробей, неопределенных коэффициентов, разложения на множители, дробно-линейных иррациональностей, Остроградского, прямые методы, интегрирование по частям, подстановки Эйлера, дифференциального бинома, интегрирования с модулем, интегральных функций, степенных, тригонометрических, гиперболических преобразований, понижения степени подынтегральной функции и группировок. Для решения определенных интегралов применяется формула Ньютона-Лейбница и нахождение пределов в точках разрыва.